Theory

Methods

All harmonization is based on the following equations.

\(\beta\): the harmonization convergence parameter

\[\begin{split}\begin{equation}\label{eqs:factor} \beta(t, t_i, t_f) = \begin{cases} 1 - \frac{t - t_i}{t_f - t_i},& \text{if } t \leq t_f\\ 0, & \text{otherwise} \end{cases} \end{equation}\end{split}\]

\(m^{rat}\): ratio-based harmoniation

\[\begin{equation}\label{eqs:ratio} m^{rat}(t, m, h, t_i, t_f) = [\beta(t, t_i, t_f) (\frac{h(t_i)}{m(t_i)} - 1) + 1] m(t) \end{equation}\]

\(m^{off}\): offset-based harmoniation

\[\begin{equation}\label{eqs:offset} m^{off}(t, m, h, t_i, t_f) = \beta(t, t_i, t_f) (h(t_i) - m(t_i)) + m(t) \end{equation}\]

\(m^{int}\): linear-interoplation-based harmoniation

\[\begin{split}\begin{equation}\label{eqs:interpolate} m^{int}(t, m, h, t_i, t_f) = \begin{cases} \frac{m(t_f) - h(t_i)}{t_f - t_i}(t - t_i) + h(t_i), & \text{if } t \leq t_f\\ m(t), & \text{otherwise} \end{cases} \end{equation}\end{split}\]

These harmonization methods are made available in aneris by name selection. Available names are listed below:

All Harmonization Methods Provided in aneris

Method Name	Harmonization Family	Convergence Year
constant_ratio	ratio	\(t_f = \infty\)
reduce_ratio_<year>	ratio	\(t_f = \texttt{<year>}\)
constant_offset	offset	\(t_f = \infty\)
reduce_offset_<year>	offset	\(t_f = \texttt{<year>}\)
linear_inerpolate_<year>	interpolation	\(t_f = \texttt{<year>}\)

Default Decision Tree

While any method can be used to harmonize a given trajectory, intelligent defaults are made available to the user. These default methods are deteremined by use of a decision tree, which analyzes the historical trajectory, model trajectory, and relative difference between trajectories in the harmonization year. The decision tree as implemented is provided below:

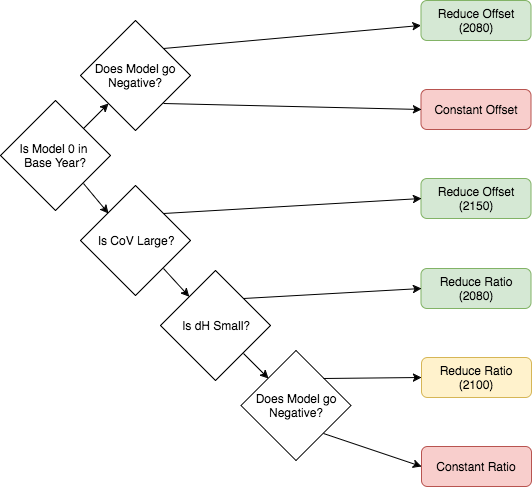
The decision tree use in aneris to determine default methods to use for each trajectory.